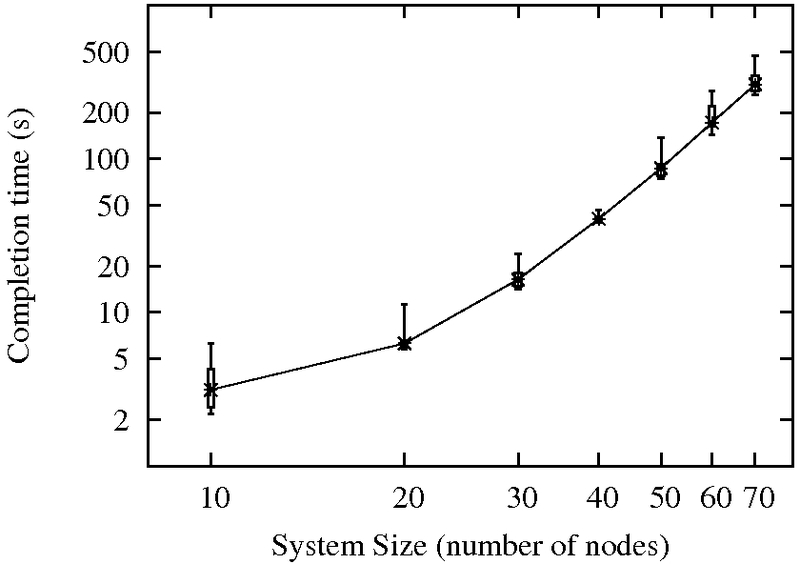
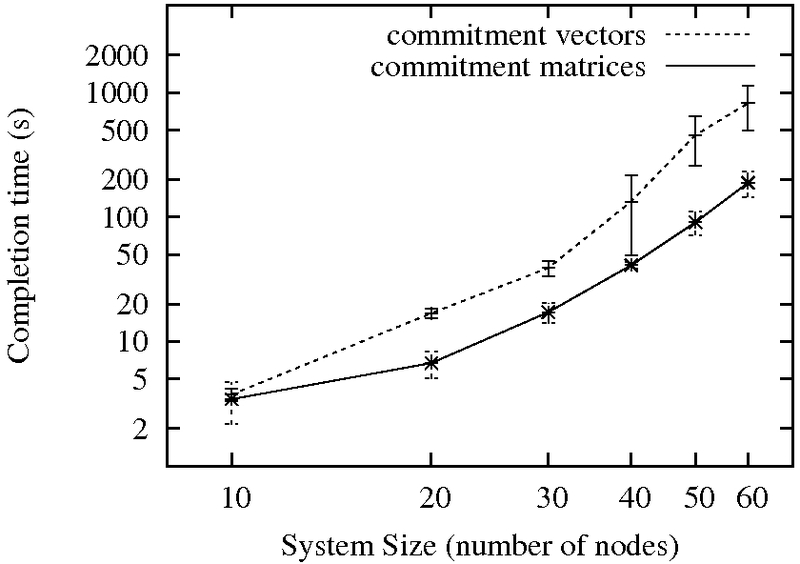
The average running time with commitment matrices with 0.95 two-sided confidence interval computed using t-distribution:

n	t	f	Running Time (seconds)	CPU Seconds/Node
10	1	3	3.43 ± 0.91	0.64 ± 0.08
20	2	6	6.71 ± 1.18	3.11 ± 0.77
30	3	10	17.16 ± 2.25	9.62 ± 1.03
40	4	13	40.98 ± 1.65	25.67 ± 0.74
50	5	17	90.69 ± 13.87	53.14 ± 5.77
60	6	20	188.32 ± 31.09	85.15 ± 4.66
70	7	24	325.31 ± 45.67	173.85 ± 28.85

The average running time with commitment vectors with 0.95 two-sided confidence interval computed using t-distribution:

n	t	f	Running Time (seconds)	CPU Seconds/Node
10	1	3	3.73 ± 0.30	1.62 ± 0.18
20	2	6	16.87 ± 1.06	8.88 ± 0.35
30	3	10	38.89 ± 3.81	23.33 ± 0.50
40	4	13	133.20 ± 59.82	54.48 ± 7.03
50	5	17	455.36 ± 139.52	96.15 ± 25.45
60	6	20	819.51 ± 228.20	263.29 ± 38.92

A quartile plot of running time with commitment matrices:

A comparision between commitment matrices and commitment vectors in terms of mean running time and standard deviation:

Download the list of nodes used for our experiment here.